How I think about LLM prompt engineering
Prompting as searching through a space of vector programs
Flashback: Word2Vec’s emergent word arithmetic
In 2013, at Google, Mikolov et al. noticed something remarkable.
They were building a model to embed words in a vector space — a problem that already had a long academic history at the time, starting in the 1980s. Their model used an optimization objective designed to turn correlation relationships between words into distance relationships in the embedding space: a vector was associated to each word in a vocabulary, and the vectors were optimized so that the dot-product (cosine proximity) between vectors representing frequently co-occurring words would be closer to 1, while the dot-product between vectors representing rarely co-occurring would be closer to 0.
They found that the resulting embedding space did much more than capture semantic similarity. It featured some form of emergent learning — it was capable of performing “word arithmetic”, something that it had not been trained to do. There existed a vector in the space that could be added to any male noun to obtain a point that would land close to its female equivalent. As in: V(king) - V(man) + V(woman) = V(queen). A “gender vector”. Pretty cool! There seemed to be dozens of such magic vectors — a plural vector, a vector to go from wild animals names to their closest pet equivalent, etc.
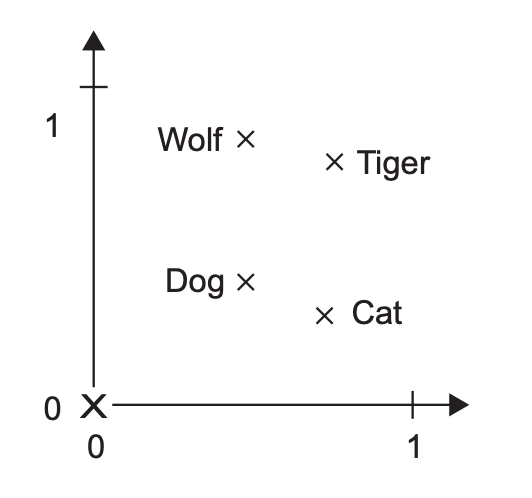
Word2Vec and LLMs: the Hebbian learning analogy
Fast forward ten years — we are now in the age of LLMs. On the surface, modern LLMs couldn’t seem any further from the primitive word2vec model. They generate perfectly fluent language — a feat word2vec was entirely incapable of — and seem knowledgeable about any topic. And yet, they actually have a lot in common with good old word2vec.
Both are about embedding tokens (words or sub-words) in a vector space. Both rely on the same fundamental principle to learn this space: tokens that appear together end up close together in the embedding space. The distance function used to compare tokens is the same in both cases: cosine distance. Even the dimensionality of the embedding space is similar: on the order of 10e3 or 10e4.
You may ask — wait, I was told that LLMs were autoregressive models, trained to predict the next word conditioned on the previous word sequence. How is that related to word2vec’s objective of maximizing the dot product between co-occurring tokens?
In practice, LLMs do seem to encode correlated tokens in close locations, so there must be a connection. The answer is self-attention.
Self-attention is the single most important component in the Transformer architecture. It’s a mechanism for learning a new token embedding space by linearly recombining token embeddings from some prior space, in weighted combinations which give greater importance to tokens that are already “closer” to each other (i.e., that have a higher dot-product). It will tend to pull together the vectors of already-close tokens — resulting over time in a space where token correlation relationships turn into embedding proximity relationships (in terms of cosine distance). Transformers work by learning a series of incrementally refined embedding spaces, each based on recombining elements from the previous one.
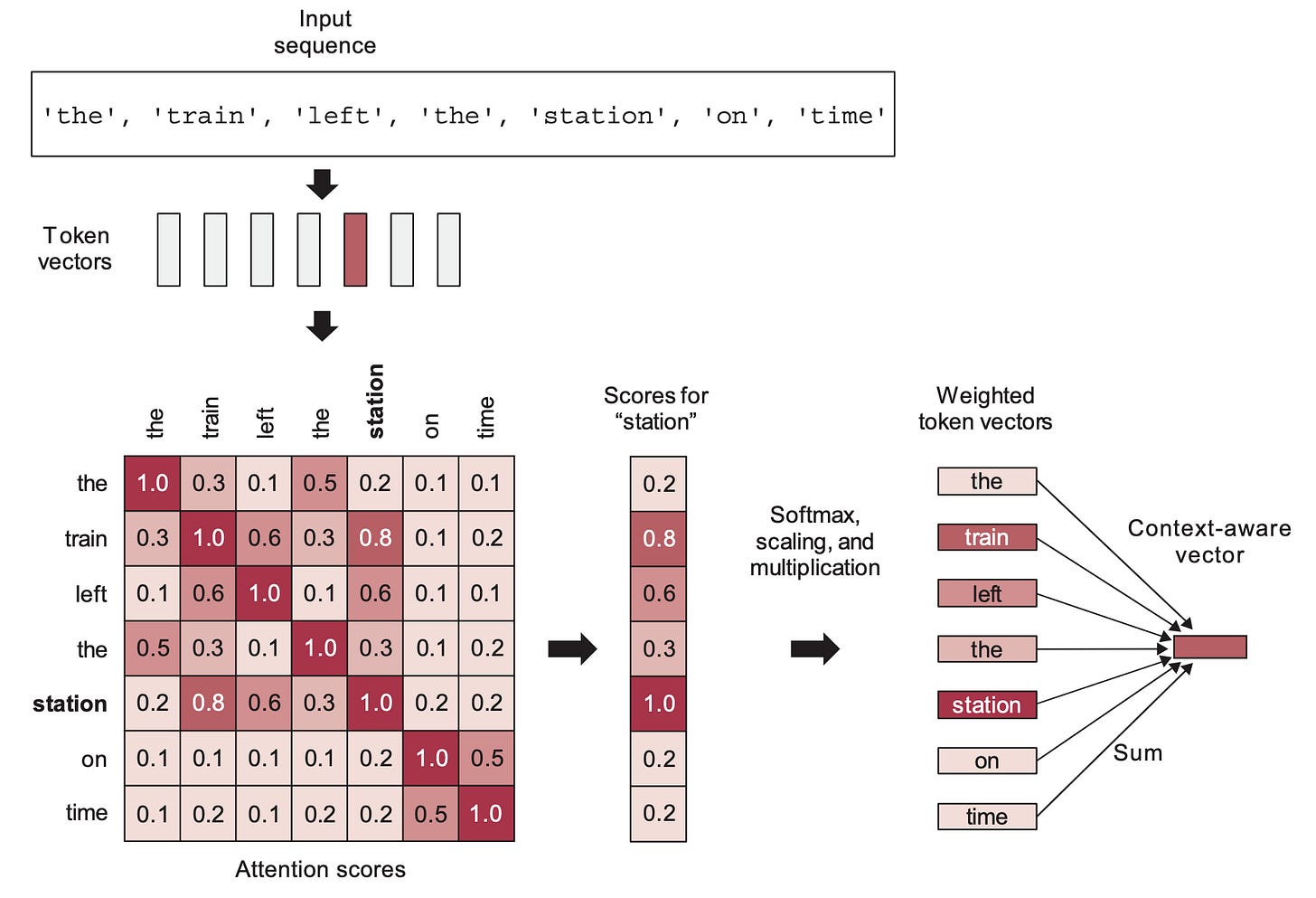
Self-attention confers Transformers with two crucial properties:
The embedding spaces they learn are semantically continuous, i.e. moving a bit in an embedding spaces only changes the human-facing meaning of the corresponding tokens by a bit. The word2vec space also verified this property.
The embedding spaces they learn are semantically interpolative, i.e. taking the intermediate point in between two points in an embedding space produces a point that represents the “intermediate meaning” between the corresponding tokens. This comes from the fact that each new embedding space is built by interpolating between vectors from the previous space.
This is not entirely unlike the way the brain learns, mind you. The key learning principle in the brain is Hebbian learning — in short, “neurons that fire together, wire together”. Correlation relationships between neural firing events (which may represent actions or perceptual inputs) are turned into proximity relationships in the brain network, just like Transformers (and word2vec) turn correlation relationship into vector proximity relationships. Both are maps of a space of information.
From emergent word arithmetic to emergent vector programs
Of course, there are significant differences between word2vec and LLMs as well. Word2vec wasn’t designed for generative text sampling. LLMs are a lot bigger and can encode vastly more complex transformations. The thing is, word2vec is very much a toy model: it is to language modeling as a logistic regression on MNIST pixels is to state-of-the-art image computer vision models. The fundamental principles are mostly the same, but the toy model is lacking any meaningful representation power. Word2vec wasn’t even a deep neural network — it has a shallow, single-layer architecture. Meanwhile, LLMs have the highest representation power of any model anyone has ever trained — they feature dozens of Transformer layers, hundreds of layers in total, and their parameter count ranges in the billions.
Just like with word2vec, LLMs end up learning useful semantic functions as a by-product of organizing tokens into a vector space. But thanks to this increased representation power and a much more refined autoregressive optimization objective, we’re no longer confined to linear transformations like a “gender vector” or a “plural vector”. LLMs can store arbitrarily complex vector functions — so complex, in fact, that it would be more accurate to refer to them as vector programs rather than functions.
Word2vec enabled you to do basic things like plural(cat) → cats or male_to_female(king) → queen. Meanwhile LLMs can do pure magic — things like write_this_in_style_of_shakespeare(“…your poem…”) → “…new poem…”. And they contain millions of such programs.
LLMs as program databases
You can see a LLM as analogous to a database: it stores information, which you can retrieve via prompting. But there are two important differences between LLMs and databases.
The first difference is that a LLM is a continuous, interpolative kind of database. Instead of being stored as a set of discrete entries, your data is stored as a vector space — a curve. You can move around on the curve (it’s semantically continuous, as we discussed) to explore nearby, related points. And you can interpolate on the curve between different data points to find their in-between. This means that you can retrieve from your database a lot more than you put into it — though not all of it is going to be accurate or even meaningful. Interpolation can lead to generalization, but it can also lead to hallucinations.
The second difference is that a LLM doesn’t just contain data. It certainly does contain a lot of data — facts, places, people, dates, things, relationships. But it’s also — perhaps primarily — a database of programs.
They’re not quite the kind of programs you’re used to dealing with, mind you. You might be thinking of deterministic Python programs — series of symbolic statements processing data step by step. That’s not it. Instead, these vector programs are highly non-linear functions that map the latent embedding space unto itself. Analogous to word2vec’s magic vectors, but far more complex.
A prompt as a program query
To get information out of a LLM, you have to prompt it. If a LLM is like a database of millions of vector programs, then a prompt is like a search query in that database. Part of your prompt can be interpreted as a “program key”, the index of the program you want to retrieve, and part can be interpreted as a program input.
Consider the following example prompt: “rewrite the following poem in the style of Shakespeare: …my poem…”
“rewrite this in the style of” is the program key. It points to a particular location in program space.
“Shakespeare” and “..my poem…” are program inputs.
The LLM’s output in the result of the program execution.
Now, keep in mind that the LLM-as-program-database analogy is only a mental model — there are other models you can use. A more common one, but less illuminating, is to think of LLMs as autoregressive text generators that output one of the most likely word sequences that could follow your prompt given the training data distribution — i.e. focusing on the task that LLMs were optimized on. You’ll understand LLMs better if you keep in mind a diversity of ways to model what they do — hopefully you’ll find this new one useful.
Prompt engineering as a program search process
Remember, this “program database” is continuous and interpolative — it’s not a discrete set of programs. This means that a slightly different prompt, like “Lyrically rephrase this text in the style of x” would still have pointed to a very similar location in program space, resulting in a program that would behave pretty closely but not quite identically.
There are thousands of variations you could have used, each resulting in a similar-yet-slightly-different program. And that’s why prompt engineering is needed. There is no a-priori reason why your first, naive program key would result in the optimal program for the task. The LLM is not going to “understand” what you meant and then perform it in the best possible way — it’s merely going to fetch the program that your prompt points to, among many possible locations you could have landed on.
Prompt engineering is the process of searching through program space to find the program that empirically seems to perform best on your target task. It's no different than trying different keywords when doing a Google search for a piece of software.
If LLMs actually understood what you told them, there would be no need for this search process, since the amount of information conveyed about your target task does not change whether your prompt uses the word “rewrite” instead “rephrase”, or whether you prefix your prompt with “think steps by steps”. Never assume that the LLM “gets it” the first time — keep in mind that your prompt is but an address in an infinite ocean of programs, all captured as a by-product of organizing tokens into a vector space via an autoregressive optimization objective.
As always, the most important principle for understanding LLMs is that you should resist the temptation of anthropomorphizing them.


